Hier kurz und knapp Hinweise für ein sicheres Passwort, sowie ein paar Informationen darüber, warum ein Passwort unsicher ist und ein anderes vielleicht nicht.
Inhaltsverzeichnis
Wie Passwörter geknackt werden
Es gibt viele Möglichkeiten, ich möchte aber nur auf zwei sehr intuitive eingehen.
Brute-Force Attacke
Brute force steht für „rohe Gewalt“ und genau das ist es: Ich möchte ein Passwort finden, also probiere ich einfach alle Möglichen Kombinationen aus. Fertig. Dauert eventuell mehrere Jahre, führt aber bei klassischen Passwörtern definitiv zum Erfolg.
Wenn man allerdings Hinweise hat (z.B.: „Das Passwort ist 8 Zeichen lang und hat am Ende zwei Ziffern“), kann man die Rechenzeit bereits dramatisch verringern (mehr dazu unten).
Wortlisten
Hier greife ich schon etwas vorweg: Manche Menschen sind so dumm und nutzen normale Wörter (zum Beispiel das Wort „Passwort“) oder Namen als Passwort! Man kann sich im Netz Wortlisten herunterladen mit z.B. 300.000 deutschen Wörtern. Das klingt nach vielen Wörtern, ein Computer kann da aber nur lachen und hat binnen Sekunden alle ausprobiert.
Wie Passwörter gespeichert werden
Ein Dienst bei den man ein Passwort hat, muss das Passwort ja irgendwie irgendwo abspeichern. Klassischerweise passiert das in einer Datenbank als Hashwert (s.u.). Angreifer haben also bei einem Hack der Datenbank nicht das Klartext-Passwort, sondern nur den Hashwert des Passwortes.
Was ist ein Hashwert?
Zu beliebigen Daten kann man mittels einer Hashfunktion einen Hashwert (oder kurz Hash) bilden, der immer aus einer festen Anzahl an bits/Zeichen besteht (z.B. 256 bit bei der Hashfunktion SHA-256). Man wandelt also Daten (z.B. ein Passwort) in einen Hashwert um. Der Clou an der Sache: Man kann den Hashwert nicht einfach wieder zurückverwandeln!
Zurückverwandeln eines Hashwertes
Man kann den Originalwert aus einem Hashwert nicht einfach so ablesen. Zum einen gibt es kein eindeutiges Ergebnis, da es pro hash-Algorithmus nur endlich viele Hashwerte gibt, theoretisch aber unendlich viele Ursprungswerte. Es kann somit zu Dopplungen (Kollisionen) kommen. Zum anderen ist das Verfahren eines (guten) Hash-Algorithmus zu komplex um einfach so den Algorithmus quasi rückwärts laufen zu lassen.
Beispiel einer Dopplung (Kollision):
Benutzen wir den Algorithmus FNV-1a, so produziert das Wort „costarring“ den Hashwert 5e4daa9d. Leider produziert das Wort „liquid“ den gleichen Hashwert. Doch warum ist das schlecht?
Sicherheit von Hashfunktionen
Angenommen ich wähle das Passwort „liquid“ und in der Datenbank wird nun der Hashwert 5e4daa9d gespeichert. Ein Angreifer bekommt durch einen Hackerangriff Zugriff auf die Datenbank und nutzt eine Wortliste zum finden des Passwortes. Er hat also den Hashwert 5e4daa9d und probiert nun alle Wörter durch. Bei dem Wort „costarring“ wird er auf einmal fündig, da es in der Liste alphabetisch höher steht als „liquid“. Er muss tatsächlich gar nicht das Original finden, sondern nur eine der Kollisionen, die existieren.
Je schwerer Kollisionen also zu finden sind, desto besser die Hashfunktion. Eine gute und viel benutzte Hashfunktion ist z.B. SHA-256.
Mehr zu Kollisionen bei Hashalgorithmen.
Kriterien an ein gutes Passwort
Jetzt haben wir also gewisses Grundwissen über Passwörter, Hashwerte und Cracking-Verfahren. Doch erschwert man es ein Passwort zu knacken?
Für die folgenden Beispiele gehe ich von einer Radeon RX570 Grafikkarte aus, welche ca. 377.000.000 (ja, ich meine tatsächlich 377 Millionen) SHA-256 Hashwerte pro Sekunde berechnen kann.
Die Länge
Kurzum: Je länger, desto besser!
Ein Szenario
Angenommen ich bin ein Angreifer und nehme an (oder weiß sogar), dass das gesuchte Passwort nur Kleinbuchstaben enthält. Für das Passwort „passwort“ bräuchte ich somit maximal ![]() Versuche. Bei 377.000.000 Versuchen pro Sekunde hat man alle Buchstabenkombinationen nach ein paar Sekunden durch, was für jeden Rechner machbar ist:
Versuche. Bei 377.000.000 Versuchen pro Sekunde hat man alle Buchstabenkombinationen nach ein paar Sekunden durch, was für jeden Rechner machbar ist:
![]()
Wählt man jedoch das Passwort „laengeristbesser“ (also 16 statt nur 8 Zeichen), so ändert sich das, denn man muss mehr potentielle Kombinationen durchprobieren: ![]() . Die Zeit der Berechnung ändert sich natürlich auch dramatisch:
. Die Zeit der Berechnung ändert sich natürlich auch dramatisch:
![]()
Das sind ca. 3.665.458 Jahre!
Egal mit welchen Optimierungen man das Knacken von Passwörtern angeht: Länger ist immer besser.
Die Zeichen
Neben der Länge sind die verwendeten Zeichen und deren Anordnung wichtig.
Ein Szenario
Ich gebe hier nur ein Beispiel an einem fiktiven Szenario:
Nehmen wir an jemand hat das Passwort „hallo123“ gewählt. Das weiß ich natürlich nicht, möchte es aber herausfinden und gehe davon aus, dass alles mögliche an Zeichen vorkommen kann. Ich bräuchte ca. 204 Tage um alle Zeichenkombinationen aus acht Zeichen auszuprobieren. Finden würde ich es vermutlich schon eher.
Nach dem Lesen der Passwort-Richtlinien des Online-Dienstes stelle ich fest, dass nur wenig Sonderzeichen erlaubt sind (nur – _ . , + * und /). Durch diese Information reduziert sich die Zeit bereits auf ca 16 Tage.
Es ist statistisch sehr sicher, dass das Passwort am Ende zwei Ziffern hat. Damit wäre ich bei 8 Stunden. Vermute ich drei Ziffern am Ende, wäre es sogar nur 1 Stunde.
Bereits hier sind wir in Bereichen, die ein Angreifer bei gewisser Motivation durchaus warten könnte (einfach den Rechner über Nacht laufen lassen und fertig).
Ich versuche mein Glück und vermute keine Großbuchstaben, da tatsächlich viele Passwörter keine enthalten. Nach 27 Minuten hätte ich das Passwort und müsste nicht mal über Nacht warten.
Ein paar weitere Gedankenspiele:
(Für ein acht Zeichen langes Passwort)
Angenommen es ist ein Wort und dann kommen zwei Ziffern: 1 Stunde und 30 Minuten
Angenommen es ist ein Wort aus Kleinbuchstaben und dann kommen zwei Ziffern: 1 Minute
Angenommen es ist ein Wort und dann drei nicht-Buchstaben (so wie „hallo123“ oder „Fuenf+-0“): 22 Stunden
Angenommen es ist ein Wort aus Kleinbuchstaben und dann drei nicht-Buchstaben (so wie „hallo123“ oder „fuenf+-0“): 0 Sekunden
Fazit
Egal welche verrückten Annahmen man trifft, bzw. auf statistischer Basis relativ sicher treffen kann: Es verkürzt die Rechenzeit dramatisch.
Je zufälliger – also „durchmixter“ – und länger ein Passwort ist, desto sicherer ist es, da man wenig Annahmen treffen kann. Man spricht dabei von hoher Entropie. Eine Zeichenketten wie z.B. „o+_jfqyF<„0f&“ hat eine hohe Entropie, ein normales Wort eine geringe.
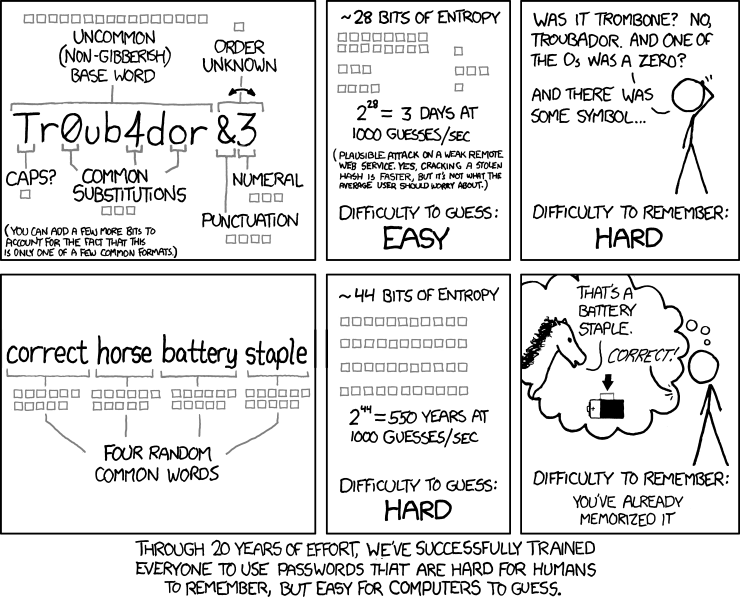 Ein sicheres Passwort finden
Ein sicheres Passwort finden
Es gibt verschiedene Mechanismen um ein sicheres Passwort zu erstellen. Es gilt aber: Einfach sich selbst was ausdenken ist unklug. Menschen sind schlecht im Erstellen von Passwörtern und tendieren dazu einfache Muster zu nutzen (z.B. Name und Zahl wie etwa „Berlin-78“). Man sollte automatische Mechanismen nutzen, wie folgt beschrieben.
Generator
Es gibt bei eigentlich allen Passwort-Managern einen eingebauten Generator für Passwörter, die z.B. auch direkt angeben wie sicher ein Passwort ist.
Wird es angezeigt, so sollte man auch eine hinreichende Qualität achten. Bei KeePass wird diese z.B. in bits angegeben, was der mathematischen Entropie (also der „Zufälligkeit“) entspricht. Ein Passwort sollte mindestens 80 bits an Entropy besitzen (entspricht in etwa einem zufälligen 14 Zeichen langen Passwort).
Diceware
Ein quasi manueller Generator ist Diceware. Dabei hat man eine Liste mit normalen Wörtern, welche alle eine Nummer haben (z.B. 43143 → multi). Die Nummer eines Wortes besteht nur aus den Ziffern 1-6 und ist genau 5 Stellen lang.
Was nützt das?
Naja jetzt nimmt man einen Würfel und würfelt fünf Zahlen und hat somit ein Wort. Das macht man beliebig häufig (empfehlenswert ist mindestens 4 mal) und hängt die Worte aneinander. Fertig ist das Passwort.
So könnte das dann aussehen:
63163 untreu
45321 ohne
32442 hohes
14355 bau
62641 undank
Wie sicher ist es?
Es gibt in der Liste ![]() unterschiedliche Wörter. Bei fünf Wörtern gibt es also für einen Brute-Force Angriff
unterschiedliche Wörter. Bei fünf Wörtern gibt es also für einen Brute-Force Angriff ![]() (über 28 Trillionen) Möglichkeiten. Bei den oben genannten 377 mio. Versuchen pro Sekunde, bräuchte man über 2300 Jahre um alle Möglichkeiten probiert zu haben.
(über 28 Trillionen) Möglichkeiten. Bei den oben genannten 377 mio. Versuchen pro Sekunde, bräuchte man über 2300 Jahre um alle Möglichkeiten probiert zu haben.
Passwörter richtig benutzen
Damit ein Passwort sicher bleibt, wenn man es mal hat, sind hier ein paar Hinweise zur richtigen Nutzung, die aber eigentlich klar sein sollten:
- Keine Passwörter mehrfach nutzen
- Keine Passwörter weitergeben (an keinen Freund, kein Familienmitglied, keine Hotline, keinen Dienstleister, …)
- Keine Passwörter übertragen (nichts unverschlüsselt per Mail, Messenger verschicken oder irgendwo ins Internet hochladen)
- Keine Informationen über das Passwort herausgeben („Acht Zeichen!? Könnte ich mir nie merken“, „Och ne, Sonderzeichen sind so umständlich zu tippen“, …)
- Keine Passwörter aufschreiben und den Zettel offen liegen lassen (kann ordentlich schief gehen)
Einfach so tun, als ob ein Passwort das peinlichste ist, was einem je passiert ist: Verschweigen und niemandem davon erzählen! 😉
